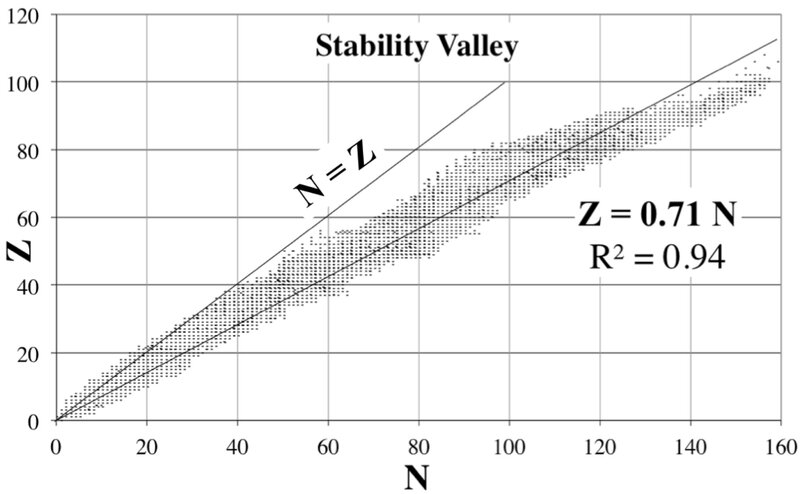
It is known since one century that nuclear energy is of the order of one million times more concentrated, in the same mass, than chemical energy.The radius of the atomic nucleus is, indeed, of the order of one million times smaller than that of a molecule. This is because the chemical and nuclear binding energies are of the same electric nature : they obey both to the Coulomb's laws, in 1/r where r is the radius of either a nucleus or a molecule. No need of a mysterious "strong force". According to Einstein, the energy of an object of mass m is E = mc². According to Bohr, the chemical energy is α²mec² . According to Schaeffer, the nuclear energy is αmc², intermediate. m is the considered mass, me the mass of the electron, α = 1/137 the fine structure constant and c the velocity of light. The so-called "strong force" (also referred to as the strong nuclear interaction or force) is the hypothetical force binding together the protons and the neutrons in an atomic nucleus. The word strong comes from the fact that the nuclear energy is around one million times greater than the chemical energy, for the same volume, dramatically demonstrated at Hiroshima. It is also known that the binding energy is around 1% of the mass energy mc². There are two well known fundamental forces in nature, the universal gravitation (formulated by Newton) and the electromagnetic force (formulated by Maxwell). It is fashionable to add two more hypothetical forces : the strong and weak nuclear forces. Very little is known about these forces.

According to the Bohr scheme, the electrons gravitate around the nucleus. The shell model assumes that the nucleons also gravitate (they don't on the graph) around a hypothetical force center. Indeed the nucleus has no nucleus around which the nucleons may orbite.
The origin of the strong force
The Rutherford scattering experiment, one century old now, consisted to collide alpha particles from a radioactive element on an atomic nucleus. The alpha particles from the radioactive element striking gold foils are scattered in different orientations. In a constant orientation, the number of particles per solid angle, called cross-section dσ/dΩ, are mesured as a function of the kinetic energy obtained by varying the number of gold foils:
 In the classical theory of 'anomalous' scattering the potential energy, where r is the separation distance from the nucleus, is represented usually in the form, where B seems to be positive:
In the classical theory of 'anomalous' scattering the potential energy, where r is the separation distance from the nucleus, is represented usually in the form, where B seems to be positive:

The problem was to find n. Bieler, a Rutherford student, imagined in 1924 a magnetic attraction equilibrating an electrostatic repulsion between the protons (this is valid for the nuclear energy as I have shown elsewhere). Here the minus sign is wrong. Indeed, the electric interaction discovered by Rutherford explains the diffusion of the α particle by an atomic nucleus. For high energies, it doesn't work, thus "explained by a mysterious "strong force". In fact, the magnetic force replaces the electric force, thus the electric 1/r Coulomb's law is replaced by the magnetic 1/r³ Poisson's law. The sign should be the same, thus positive instead of negative as hypothesized. The graph shows the electric part (1/r law) discovered one century ago by Rutherford and the not so anomalous magnetic part (1/r³ law), discovered by me:
 The coordinates of this graph are both logarithmic, giving straight lines with -2 and -6 slopes due to the Rutherford formula where the potential exponents are multiplied by 2:
The coordinates of this graph are both logarithmic, giving straight lines with -2 and -6 slopes due to the Rutherford formula where the potential exponents are multiplied by 2:

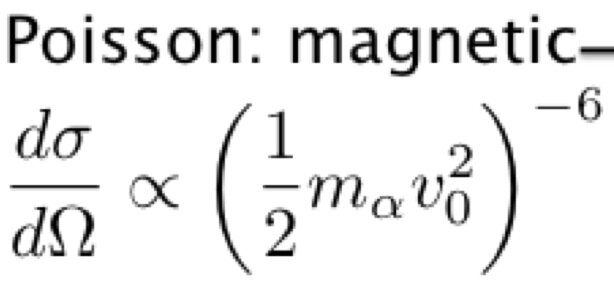
Binding energy
The binding energy per nucleon is given by the formula
BE/A = (Z mp + N mn - M)/A
where Z is the atomic number, N the neutron number and A = Z + N is the atomic mass number. M, mp, and mn are the masses of one nucleus (approximately of an atom), one proton and one neutron.
At a time when the neutron was not discovered, Aston used the packing fraction given by the formula:
f = (M - A)/A
where M is the mass of the atom measured experimentally and A the atomic number.
The Shell Model or Independent-particle Model or Hartree Model
The official mainstream physics model of the atomic nucleus is the shell model which the atomic model of Bohr and continuators adapted to the atomic nucleus.
The electrons are replaced by the nucleons. There are two kinds of nucleons, protons, electrically charged, and neutrons, uncharged. Contrarily to the atom, the nucleus has no nucleus. This deficiency is circumvented by the bold assumption that each nucleon experiences a central attractive force which can be ascribed to the average effect of all the other nucleons in the nucleus. On this assumption, each nucleon behaves as though it were movins independently in a central field, which is described as short-range potential well. Secondly, this potential is assumed to be the same for all values of l, the angular momentum quantum number of the nucleons. In the assumed central potential, each nucleon is imagined to be capable of describing an orbit of well-defined energy and angular momentum, in a manner analogous to the behavior of atomic electrons.
This assumption seems to be in conflict with the strong interaction between nucleons, as seen experimentally, and in nuclear reactions generally. This weak interaction paradox was solved by using the Pauli exclusion principle. The expected strong interaction may be present but unable to manifest itself because all the quantum states into which the nucleon might be scattered are already occupied…
The main characteristic of the shell model is the so-called "magic numbers" (Z and/or N = 2, 8, 20, 28, 50, 82, 126) corresponding to the atomic levels.
The Liquid drop Model or Semi-empirical Mass Formula
The liquid drop model is the antithesis of the independent-particle model. The interactions are assumed to be strong instead of weak. The initial assumptions are (Evans p. 365) :
1. The nucleus is like a droplet of incompressible matter, and all nuclei have the same density.
2. Forces between nucleons are considered to be spin-independent as well as charge-independent if the coulomb force is turned off.
3. These nuclear forces have a short-range character and are effective only between nearest neighbors. Each nucleon interacts with all its nearest neighbors.
4. The volume or exchange energy is proportional to to the number of nucleons A for A ≥ 16, giving a radius R0 A1/3, where R0 is a constant.
5. The surface energy is like the surface tension of a liquid due to the fact that nucleons at the surface have fewer near neighbors than nucleons that are deep within the nuclear volume. We can expect a deficit of binding energy for these surface nucleons. A simple calculation shows that the surface energy is proportional to A2/3.
6. The Coulomb repulsion energy between protons is the only known long-range force in nuclei. The total nuclear charge Ze is assumed to be spread approximately uniformly throughout the nuclear volume. Again assuming a constant-density nuclear radius R0 A 1/3 and applying the Coulomb law for the potential, the Coulomb energy is proportional to Z2/A1/3.
7. The asymmetry energy, the deficit in energy dependent on the neutron excess or deficit, is (N - Z)2/A = (A - 2Z)2/A.
8. The pairing energy δ is a correction to take into account the pairing of N and Z.
The complete Bethe-Weizsäcker formula is



The following graph shows the Bethe-Weizsäcker curve (in blue), compared with the experimental data (in red) for the N = Z nuclei. The BW formula is unable to represent the binding energies of even Z and even N. There is also no distinction for same A nuclei with even N - odd Z and even Z - odd N (mirror nuclei).
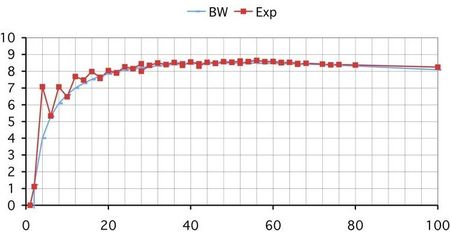
Atomic number in abscissas and binding energy per nucleon in ordinates
Four-shell structure or α particle model
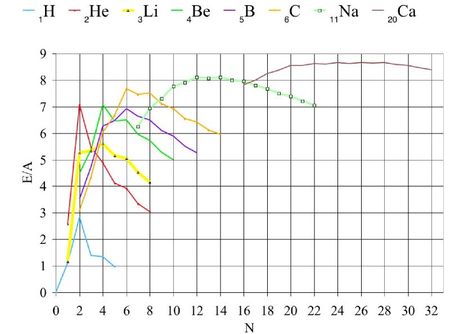
This type of models have been initiated by Gamow who observed that the nuclei with atomic masses multiple of 4 have larger binding energies. Indeed, it can be observed peaks of the binding energies for even A, Z and N. It is maximum for both N and Z even. The addition of an α-particle adds a tetrahedron to the structure already existing and so three bonds are alloted per addition.
For example, the maximum of ³Li is smaller than for both ²He and ⁴Be. For given Z, peaks appear for even N. They are greater if Z is also even. The amplitude diminishes when Z increases. The peaks are small but detectable even for the heavy nuclides:

Binding energies of 2,000 nuclides (Excel, to be downloaded)
2,000 nuclides
Supercomputer calculations
The following curve shows the helium isotopes total binding energies, experimental and "ab initio", calculated by a supercomputer . It shows that the total binding energy is practically constant, except for the pairing effect, for the N>2 isotopes of helium. The discrepancy with the experimental values is attributed to the "3 body force". In fact, a better approximation is obtained by assuming that the excess neutrons are unbounded (halo nuclei). The red horizontal line is nearer to the experimental values (in red) than the super computer calculated orange line. Moreover, it seems that 4H (alpha particle) has not been calculated at all : the -28 MeV is the experimental value of its total binding energy. Even the simplest bounded nucleus (2H, the deuteron or heavy hydrogen) has never been calculated "ab initio". The fundamental laws and constants of the so-called "strong force" are still inexisting after one century of nuclear physics.
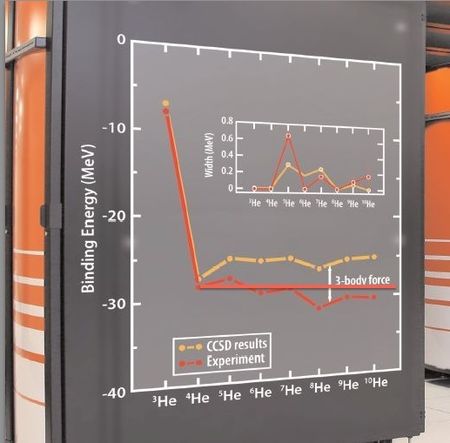
Figure 5. ORNL's Jaguar, the world's second fastest computer, enables certain nuclear calculations only dreamt of a few years ago. As an example, Jaguar was used for the first ever ab initio computation of neutron-rich helium nuclei using coupled cluster theory (shown in the figure on the side of the computer). The figure shows the binding energy of these nuclei, while the inset indicates the width, related to lifetime. Experimental data are marked in red. The calculated masses show a systematic deviation from experiment; this can be attributed to a three-body force, missing in the calculation. (original legend)
Energy per proton
Dividing the total binding energy by the the proton number, one obtains the following curves. From selected elements of the atomic mass table, one sees that the binding energy per proton tends towards a limit for each chemical element :
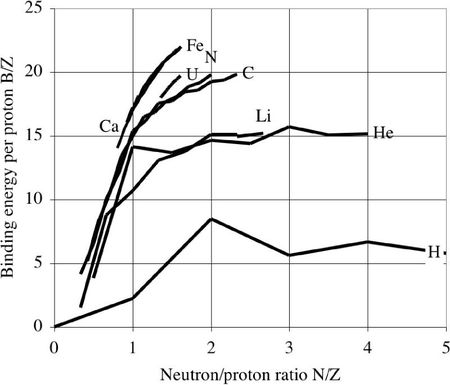
This limit is maximum for Fe and neighbors. For heavier nuclides, the binding energy decreases, due to the Coulomb repulsion between the protons.
Electromagnetic theory of the nuclear force
It is believed since almost a century that the strong force cannot be electromagnetic. This is incorrect because the nucleus has no nucleus or, in other words, the angular momentum has no fixed point like the atom. Therfore such a nucleus cannot be stable. The proof is given by my calculations ("Electromagnetic Theory of the Binding Energy of the Hydrogen Isotopes", J Fusion Energy (2011) 30 :377-381 here).
Deuteron binding energy
For the simple case of the deuteron, I have obtained the following formula:
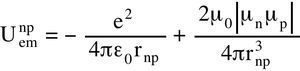

If you have studied electromagnetism you will recognize the Coulomb attractive force and the magnetic repulsive force. Graphically, it gives the electromagnetic nuclear potential similar to other phenomenological potentials but truly ab initio because it contains only universal constants:

The formula in the graph is the same as the previous one but with different universal constants. One may recognize the famous mc² formula for the mass energy. It is multiplied by the fine structure constant α = 1/137. RP is the proton Compton radius. gp and gn are the Landé factors of the proton and of the neutron.
A better precision is obtained with a graphical resolution taking into account both electric charges in the neutron. Comparison is given below :
The curve at the right is the same as above. The scales are to be divided by 100. This is the first ab initio calculation of the binding energy of a nucleon (ab initio means a calculation using only fundamental constants, without adjusting parameters, and a well established theory e.g. Maxwell theory of electromagnetism).
Binding energy of the hydrogen isotopes
The binding energies of all the hydrogen isotopes have been calculated assuming the following structures:
Simplified calculation for H and He nuclei with N > 2
 This method has been simplified for the hydrogen (giving the same results) and helium isotopes with N > 2. It is assumed that the total binding energy is the same when the number of nucleons is larger than 2, due to the small binding energy of the excess neutrons. These nuclei are called halo nuclei. The 4He binding energy is too low, probably due to the neglect of the positive charge of the neutron. More precise calculations are necessary for 4He. One can see that the binding energies of the N>2 isotopes are parallel to the experimental curves, justifying the approximation of almost zero binding energy of the last neutron (halo nuclei).
This method has been simplified for the hydrogen (giving the same results) and helium isotopes with N > 2. It is assumed that the total binding energy is the same when the number of nucleons is larger than 2, due to the small binding energy of the excess neutrons. These nuclei are called halo nuclei. The 4He binding energy is too low, probably due to the neglect of the positive charge of the neutron. More precise calculations are necessary for 4He. One can see that the binding energies of the N>2 isotopes are parallel to the experimental curves, justifying the approximation of almost zero binding energy of the last neutron (halo nuclei).
Nuclear to chemical energy ratio
The electromagnetic theory of the nuclear energy shows that it is αmc² or 1/137 of the mass energy, known to be of the order of 1%.
It is well known that the chemical energy is given by the Rydberg constant from the Bohr theory of the atom, ½α²mec² where me is the masses of the electron and α the fine structure constant.
The electromagnetic theory gives also the nuclear to chemical energy ratio, for the same weight, as
α-1mp/me = 137 x 1836 = 250,000
where mp and me is the mass of the proton. This formula, a consequence of the electromagnetic theory, explains for the first time why the nuclear energy is up to one million times more concentrated than the chemical energy, for the same volume.
My presentation about the Strong_Force, and the calculated binding energies of hydrogen and helium binding energies H and_He_energies, may be downloaded.
Simple derivation of the nuclear to chemical energy ratio
It is known since one century that radium releases a huge energy, one million times larger than any combustion energy, according to Pierre Curie and others. This is the reason why nuclear energy is expressed in MeV and chemical energy in eV. "The energy stored by the binding energy of the outer electrons to the nucleus is, inversely, very much smaller (a hundred thousand or even a million times smaller), than that stored in the binding of nucleons in the nucleus. I have often been asked why it is that the smallest particles carry the largest energy. The precise analysis of this relation would lead us too far." Using this suggestion, we shall compare theoretically the radius and energy ratios of the hydrogen atom and the deuteron nucleus. The Bohr radius of the hydrogen atom is :

where
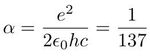
is the fine structure constant, representing the strength of coupling between radiation and matter, appearing also in the nuclear cross section. h is Planck's constant, me, the electron mass and c, the light velocity.

H atom and 2H nucleus. - Comparison between electron and neutron distances. a0 is the Bohr radius and RP is the proton Compton radius identified with the proton radius.
There exists no formula, using fundamental constants only, for the radius of a nucleon. Therefore we shall use the proton Compton radius RP, five times smaller than the experimental value of the proton radius but of the same order of magnitude, knowing that the binding energy per nucleon varies from one to ten times from deuteron to iron :
where mp is the proton mass. In the deuteron, the distance between the centers of the neutron and the proton being 2RP (figure), one obtains an expression of the ratio of the separation distances of the electron and of the neutron from the proton :

The separation energy of a neutron from a proton is 2.2 MeV and 13.6 eV for an electron from a proton, giving a 163,000 ratio. The Bohr formula of the binding energy of the fundamental state of the hydrogen atom is :
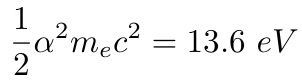
Multiplying by a0 / (2RP) from equation above, one obtains the binding energy of the deuteron :

This value was already obtained with an electromagnetic method. It is 30 % smaller than the experimental value, 2.2 MeV. A more precise result with a three body formulation (unpublished) gives a precision of 5 %.
Dropping the 1/4 coefficient, one obtains a mean value of the order of magnitude of the nuclear binding energy per nucleon :
which is coincidentally almost that of the alpha particle, 7.02.
This calculation explains why the binding energy of the nuclei is between 0.1 % and 1 % of the mass energy, or, per nucleon, between 1 MeV for the deuteron and 10 MeV for iron.This simple calculation confirms that the order of magnitude of the binding energy of a nucleus can be found theoretically from first principles and fundamental constants without ad hoc constants.
Poster: (click to enlarge or, better, unload it)

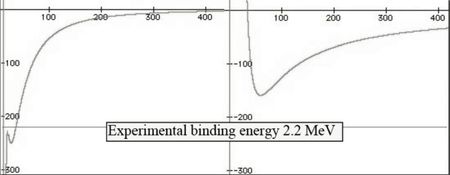
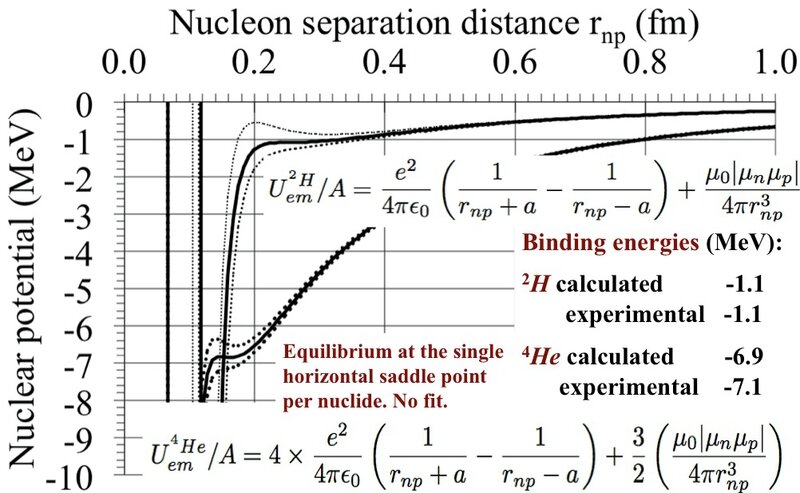
 Assuming that the deuteron 2H has one proton with one +e charge and one neutron +e and -e charges, separated by 2a, adjusted to the single horizontal inflection point. The electric attraction is equilibrated statically by the magnetic repulsion, function of the neutron-proton separation distance rnp and the electric 2a charges separation. As by chance, the binding energies of 2H and 4He coincide with their horizontal inflection points.
Assuming that the deuteron 2H has one proton with one +e charge and one neutron +e and -e charges, separated by 2a, adjusted to the single horizontal inflection point. The electric attraction is equilibrated statically by the magnetic repulsion, function of the neutron-proton separation distance rnp and the electric 2a charges separation. As by chance, the binding energies of 2H and 4He coincide with their horizontal inflection points.












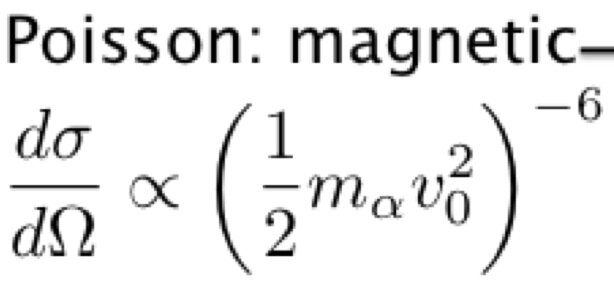





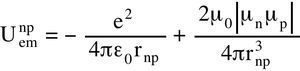





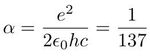



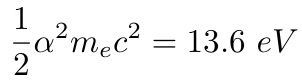





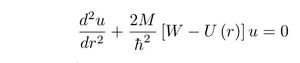


/https%3A%2F%2Fprofilepics.canalblog.com%2Fprofilepics%2F2%2F5%2F251882.jpg)