ANOMALOUS RUTHERFORD SCATTERING IS MAGNETIC

The physical nature of the nuclear interaction has been discovered to be electromagnetic.


The atomic nucleus was discovered by Rutherford, explaining electrically nuclear scattering, with a slope -2 in log-log coordinates. For high kinetic energies, the slope is -6, magnetic:

The Rutherford scattering is electromagnetic. Details here: Rutherford
 
NUCLEAR BINDING ENERGY IS ELECTROMAGNETIC

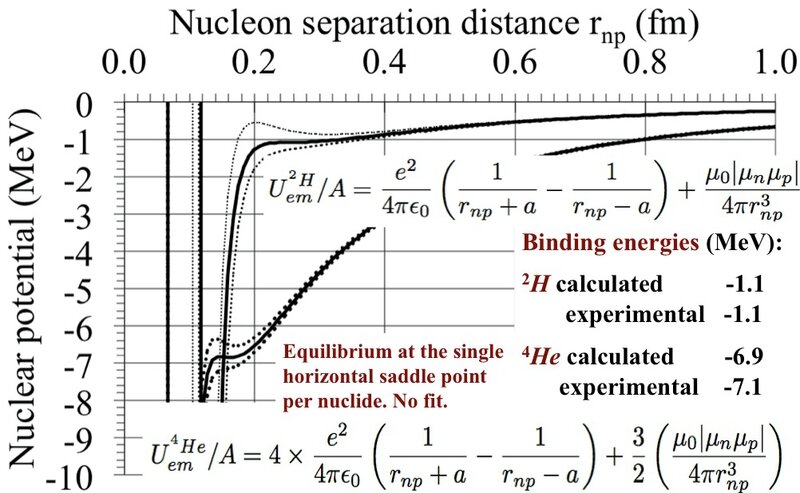
A proton attracts a not so neutral neutron as a rubbed plastic pen attracts small pieces of paper. Quantitatively, one has to use the exact dipole formula shown on the graph and not the approximate 2a/r²  (cf Feynman vol. 2, § 6-2, formula 6.8). The binding energies of  ²H and ⁴He nuclei have been calculated, WITHOUT FITTING, from the STATIC equilibrium between the attractive 1/r electric Coulomb potential and the repulsive short range 1/r³ magnetic Poisson potential. As shown on the graph below, the saddle points coincide with the ²H and ⁴He experimental nuclear binding energies:

 The nuclear energy is electromagnetic, details here: AEM

After one century of modern phenomenological formalism, the binding energy of even the simplest bound nucleus, the deuteron, remains a puzzle: charge independence, centrifugal barrier, strong force with strength 1, magic numbers, unobservable observables, virtual particles, exchange forces, ab initio… The nucleus having no nucleus, nucleons cannot orbit as the electrons:

The agreement between electromagnetic theory and experiment is significant for both electric and magnetic (not so anomalous) Rutherford scattering and also for the (not so strong) nuclear interaction.

AN EXAMPLE OF INTERESTING CRITICS (No comment):

This paper concerns my calculation with Schrödinger equation, later published in China: WJNST_Schrodinger

Manuscript #2013-1465RR:

Editor's Comments:


Reviewer Comments:
Reviewer #1 Evaluations:
RECOMMENDATION: Reject
Original Paper required: Yes
Well Organized and Clear required : Yes
Free From Errors required : No
Conclusions Supported required : No
Satisfactory English required : Yes
Appropriate Title required : Yes
Good Abstract required : Yes
Clear Figures required : Yes
Adequate References required : Yes

Reviewer #1 (Comments to the Author required ):

I have read the rebuttal comments carefully. I am afraid that my objections were not adequately addressed and serious problems remain.

Regarding the more general and issues relevant to this work:

It is an experimental fact (explained or not) and a very basic and important one in nuclear phenomenology, that the force between two protons, two neutrons or a proton and a neutron is almost the same except for an electromagnetic part. If a theoretical model contradicts the observed fact, then the theoretical model is wrong. In this work no effort has been made to explain the almost equal force in the three cases and in fact the rebuttal document seems to dismiss the question as a detail.

It is maintained that the present theory is more fundamental (in any case, simpler indeed) than QCD and hence preferable. Now, a sphere is a more fundamental and elegant shape than the shape of a cow's body, which is largely determined by her bone structure and flesh. Should we represent our cow as a sphere and expect her to simply roll down the hill - then birch her for failing to do so?

It is also pointed out that the number of parameters in empirical nucleon-nucleon potentials is ridiculous. I definitely sympathize. Nuclear theorists would kill (so to say) for a simpler nuclear potential, but this is what nature gave us, explained or not. We can't make it go away.

To ensure that I would not judge unfairly based on epistemological arguments only, I took some time to check the calculations more closely. Unfortunately, I found genuine and fundamental errors and misconceptions.

For example:

In Eqs. (11) and (15), E is the eigenenergy of a solution to the respective Schroedinger equations. These E's should be constants, namely, all r-dependent terms should vanish. That indeed leads from (11) to (13), while for (15) it means that the last term should vanish. What went wrong? The exponential function exp^{-r/b} was wrongly assumed to be an eigenfunction for the corresponding Schroedinger equation. But it is not. The potential is different from that in the Hydrogen atom and the eigenfunction's radial dependence is different too.

The minimum of the quantity E(r,b) or E(a,b,r) is meaningless. The eigenenergy shall not be a function of r. The meaningful result in the context of quantum mechanics would be the eigenenergy and the eigenfunction (and the corresponding density).

I estimate also that, for the neutron polarization vector to have a length of the order of 0.1 fm (cf quantity a in Fig.2), and for an electric field at a distance comparable to the deuteron size, the neutron polarizability required would be at least 10 times larger than the value extracted experimentally (which is about 10^-3fm^3).

Unfortunately, I find the present work scientifically unsound and unsuitable for publication.

.