Forces between nucleons according to Evans
Chapter 10 Forces between nucleons
1. General Characteristics of Specifically Nuclear Forces
a. Comparison of Atomic and Nuclear Forces
"no predominant central particle" : the nucleus has no nucleus like the atom
The forces have a very short range of action: the measurement of the range of action is undefined, unlike the radioactive decay period.
"In order to confine a nucleon to a region of this size, (…) its kinetic energy must be of the order of (…) 20 MeV. There is no experimental proof that the nucleons should have an orbital movement. Is there an orbital movement of the atoms in a molecule or a crystal? No. The usual shell model is an adaptation of the atomic model of Bohr and followers not necessarily applicable to the atomic nucleus.
b. Inadequacy of Classical Forces
"the total binding energy of nuclei is proportional to the number of nucleons A and not to A²". This is well known in chemistry and crystallography.
"The electrostatic potential energy between the same two nucleons is identically zero because the neutron is uncharged". The neutron is not uncharged, it contains electric charges with no net charge.
c. The Singlet and Triplet Forces between Nucleons
"Because the nucleons are fermions and obey the Pauli exclusion principle, there can be involved at most two neutrons (spin "up" and spin "down") and two protons in such a group". Nothing to say about it, except that there exists no physical explanation of the exclusion principle and its applicability to the nucleons.
"The possible forces therefore include three types of singlet forces (antiparallel spins) (…) The triplet forces (parallel spins) are restricted to one type for S states" Not very clear.
"The (pp) force represents the specifically nuclear attractive force between two protons and do not include their purely classical coulomb interaction". What is the experimental basis?
"That there exists also a strong attractive force (nn) between neutrons is shown by the fact that the neutron excess (N - Z) in nuclei varies approximately as A5/3 and appears to counterbalance the disruptive coulomb forces in heavy nuclei". Although this law (Evans p. 272) is somewhat better than the linear correlation, it is not a proof of the existence of the strong force.
d. Exchange Forces
"The clear experimental evidence that nuclear forces show saturation directs our attention toward the purely quantum-mechanical concept of exchange forces". This is a strange idea. Saturation is not specific to the nucleus: it exists also in crystals like NaCl. In fact saturation is common in all materials where the chemical binding energy is proportional to the mass.
1. "Heisenberg forces in which there is an exchange of both the position and spin coordinates of the two interacting nucleons" Strange hypothesis.
"Heisenberg forces are ruled out by the clear experimental fact that the α particle is the saturation subunit". I would better say that the nucleons with Z and N larger than 2 contain α particles.
2."Majorana forces,in which there is exchange of the position coordinates but not of spin. Variant of Heisenberg forces.
3. "Bartlett forces, in which there is exchange of the spin coordinates but not of the position coordinates". Variant of Heisenberg forces.
e. Tensor Forces
"With central forces, the probability density of nucleons S states must be spherically symmetric". Of course.
"the strength of this noncentral force, or tensor force, depends not only on the separation between the interacting pair of particles but also on the angle between the spins of the particles and the line joining the particles, like the force between two magnets". This force may be actually magnetic, not only a imitation.
"some other small effects are explicable if there is admixed with the dominant central force a small amount of a noncentral force." This is a second order effect, the first order effect needs the knowledge of the universal constants characterizing the nuclear forces, still unknown.
f. Charge Independence of Singlet Forces between Nucleons
"It is found that the singlet forces between all pairs of nucleons are substantially equal, i.e. ¹(np) = ¹(nn) = ¹(pp)".
No information given about the experimental method used to obtain this result.
2. Ground Level of the Deuteron
a. Wave Function for the Rectangular-well Approximation
"For simplicity, we may choose at first the rectangular potential well, of depth D and radius b (…) where r is the distance between the proton and neutron. (…) The radial wave equation for the relative motion becomes
where M is the reduced mass of the proton and neutron (…). and W is their total energy (…). For the ground level of the deuteron, the total energy W is restricted to the single constant value W = - B where B =2.225 MeV is the observed binding energy of the deuteron". The calculation continues to obtain "the rationalized de Broglie wavelength λ of the relative motion of two particles having reduced mass M and sharing kinetic energy equal to the binding energy B of the deuteron".
This binding energy has never been calculated. Calculations improperly called ab initio never use universal constants because the universal constants of the nuclear forces are unknown.
Chapter 11 Models of Nuclei
1. Summary of Experimental Evidence Which Should Be Represented by the Model
1. Nuclear angular momenta I of ground levels
For even-Z even-N nuclides, I=0.
For odd-Z odd-N nuclides, I = 1, 2, 3,…
For odd-A nuclides, I = ½, 3/2…
Mirror nuclei have equal I.
Extremes of triads have equal I.
No justification is given. Odd-A nuclides are of two different kinds : odd-Z even-N and even-Z odd-N. The independent parameters of a nucleus are N and Z, not A which is composite.
2. Magnetic dipole moments μ
They are summarized in Schmidt diagrams. Very low precision, due to theory or to measure?
3. Electric quadrupole moments Q
Systematic empirical variation with Z or N.
4. Existence of isomers
Statistical concentration in "islands of isomerism".
5. Relative parity of nuclear levels
As seen in β and γ decay.
6. Discontinuities of nuclear binding energy
and of neutron or proton separation energy, as seen for particular values of N and Z, especially 50, 82 and 126. These discontinuities at the so-called "magic numbers" are relatively small and diffuse.
7. Frequency of stable isotones and isotopes
Statistical concentration for particular values of N and Z (Chap. 8, Fig. 3.1?).
8. Pairing energy for identical nucleons
as seen in the occurrence of stable, nonadjacent, isobars (Chap. 8, Fig. 3.3). They correspond to a sequence of completed "four-shells" and suggest an α model for light nuclei (p. 298, Chap. 9, Fig. 3.1). They are very large for the light nuclei, particularly around ⁴He. They are very small but still detectable for the heaviest nuclides. There are peaks for even N independently of Z parity and also foreven Z independently of N parity.
9. Constant density of nuclei
10. Neutron excess N-Z dependent on A5/3
2. The Nuclear Shell Model
a Assumptions in the Independent-particle Model
In contrast with the situation with atoms, the nucleus contains no central bodywhic can act a force center. This deficiency is circumvented by the bold assumption that each nucleon experiences a central attractive force which can be ascribed to the average effect of all the other (A - 1) nucleons in the nucleus. On this assumption, each nucleon behaves as thought it were moving independently in a central field which is described as a short range potential well.
The Weak-interaction Paradox for Low-lying States.
"In the assumed central potential, each nucleon is imagined to be capable of describing an orbit of well-defined energy and angular momentum, in a manner analogous to the behavior of atomic electrons. (…) Thus it is possible to accept the model of weak interaction between the constituent nucleons within a nucleus at low excitation energies, without denying the inherently strong character of the interaction between free nucleons."
b. The Sequence of Nucleon States for the Ground Levels of Successive Isotopes and Isotones.
"The value of the independent-particle model lies mainly in its ability to give a nearly correct energy sequence for nucleon states having different values of the orbital angular momentum l. A simple rectangular well having a great depth and a radius about equal to the nuclear radius R is a sufficiently good representation of such a short-range force."
"Therefore, in each state of a given I, there can be (21 + 1) identical nucleons when spin is neglected or 2(21 + 1) identical nucleons if the energy is independent of spin orientation. The order of energy states for the deep rectangular well turns out to be 1s, 1p, 1d, 2s, 1f, 2p, 1g with 2, 8, 18, 20, 34, 40, 58 nucleons. This sequence fails to give any indication of a closed shell at 50 nucleons and fails even more clearly for still larger nucleon numbers. With more assumptions it is possible to match the higher magic numbers 50, 82, and 126, called major closed shells. The shell model, "periodic system for nuclei", with strong spin-orbit coupling, gives the first satisfactory representation of the angular momentum, parity, and magnetic dipole moment of the ground levels and the lowlying excited levels of nuclei. "

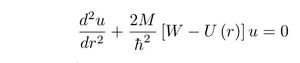


/http%3A%2F%2Fstorage.canalblog.com%2F32%2F06%2F1391198%2F108815869_o.jpg)
/http%3A%2F%2Fstorage.canalblog.com%2F09%2F70%2F1391198%2F107453210_o.jpg)
/http%3A%2F%2Fstorage.canalblog.com%2F47%2F59%2F1391198%2F106941812_o.jpg)
/http%3A%2F%2Fstatic-content.springer.com%2Fcover%2Fjournal%2F10894%2F30%2F5.jpg)
/https%3A%2F%2Fprofilepics.canalblog.com%2Fprofilepics%2F2%2F5%2F251882.jpg)